 login/create account
login/create account
Non-separable center of a lattice (Solved)
I will call center 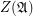 of a bounded distributive lattice
of a bounded distributive lattice 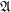 the sublattice of all complemented elements of
the sublattice of all complemented elements of 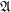 .
.
I will call a bounded distributive lattice 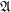 a lattice with separable center when
a lattice with separable center when 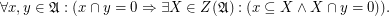
Equivalently a bounded distributive lattice with separable center is such a bounded distributive lattice 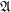 that
that 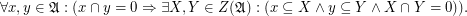
Conjecture There exist bounded distributive lattices which are not with separable center.
(Previously this problem was erroneously stated without the word distributive, it is corrected now.)
This conjecture follows from William Elliot's post in sci.math and the criterion of a lattice to be distributive, see here.
So the problem solves positively.
Admins: Should I delete this problem from Open Problem Garden because its solution was too easy (found in less than one day). Or just to leave it marked as solved?
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University