 login/create account
login/create account
Distribution and upper bound of mimic numbers
Problem
Let the notation 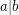 denote ''
denote '' divides
divides  ''. The mimic function in number theory is defined as follows [1].
''. The mimic function in number theory is defined as follows [1].
Definition For any positive integer 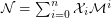 divisible by
divisible by 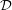 , the mimic function,
, the mimic function, 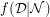 , is given by,
, is given by,
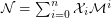 divisible by
divisible by 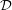 , the mimic function,
, the mimic function, 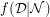 , is given by,
, is given by,
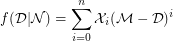
By using this definition of mimic function, the mimic number of any non-prime integer is defined as follows [1].
Definition The number  is defined to be the mimic number of any positive integer
is defined to be the mimic number of any positive integer 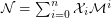 , with respect to
, with respect to 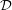 , for the minimum value of which
, for the minimum value of which 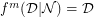 .
.
 is defined to be the mimic number of any positive integer
is defined to be the mimic number of any positive integer 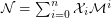 , with respect to
, with respect to 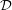 , for the minimum value of which
, for the minimum value of which 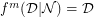 .
. Given these two definitions and a positive integer 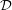 , find the distribution of mimic numbers of those numbers divisible by
, find the distribution of mimic numbers of those numbers divisible by 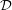 .
.
Again, find whether there is an upper bound of mimic numbers for a set of numbers divisible by any fixed positive integer  .
.
Bibliography
*[1] Malay Bhattacharyya, Sanghamitra Bandyopadhyay and U Maulik, Non-primes are recursively divisible, Acta Universitatis Apulensis 19 (2009).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University