 login/create account
login/create account
Problem Let 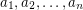 be natural numbers with
be natural numbers with 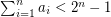 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 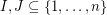 with
with 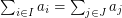 . Is it possible to find such a pair
. Is it possible to find such a pair 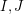 in polynomial time?
in polynomial time?
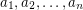 be natural numbers with
be natural numbers with 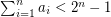 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 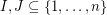 with
with 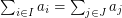 . Is it possible to find such a pair
. Is it possible to find such a pair 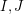 in polynomial time?
in polynomial time? This is one of a class of search problems for which a positive solution is garaunteed (so the corresponding decision problem is trivial) based on a theoretical property of the problem. Another such problem is given a Hamiltonian cycle in a cubic graph, find a second Hamiltonian cycle (here a theorem of Smith guarantee's a positive solution). The above problem is particularly attractive, since the proof that a pair 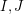 must exist is quite simple, but it gives no insight into how to find the pair
must exist is quite simple, but it gives no insight into how to find the pair 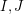 .
.
It seems to be consensus among the cryptography community that this problem is hard.

 Drupal
Drupal CSI of Charles University
CSI of Charles University