Open Problem Garden

Importance: High ✭✭✭

Author(s):	Diestel, Reinhard
	Leader, Imre

Subject:	Graph Theory
	» Infinite Graphs

Keywords:	binary tree
	infinite graph
	normal spanning tree
	set theory

Recomm. for undergrads: no

Posted	by:	mdevos
	on:	June 26th, 2008

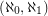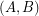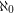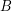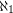Call a graph an $(\aleph_0,\aleph_1)$ -graph if it has a bipartition $(A,B)$ so that every vertex in $A$ has degree $\aleph_0$ and every vertex in $B$ has degree $\aleph_1$ .

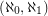Problem Characterize the $(\aleph_0,\aleph_1)$ -graphs.

The motivation for this problem comes from a lovely paper of Diestel and Leader [DL] where they prove that an infinite graph has a normal spanning tree (the natural infinite analogue of a depth-first search tree) if and only if it has no minor isomorphic to either an 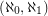$(\aleph_0,\aleph_1)$ -graph or an Aronszajn tree. (An earlier conjecture of Halin asserted that only the first of these excluded minors was needed.) So, 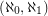$(\aleph_0,\aleph_1)$ -graphs appear as a forbidden minor obstruction to the existence of a kind of depth-first search tree for infinite graphs.

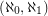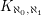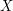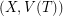The obvious example of an $(\aleph_0,\aleph_1)$ -graph is $K_{\aleph_0,\aleph_1}$ , but there are other natural families of such graphs. For instance, let $T$ be an infinite binary tree with root $r$ , and let $X$ be the set of all rays (one way infinite paths) with endpoint $r$ . Now, form a bipartite graph with vertex bipartition $(X,V(T))$ and adjacency given by the rule that 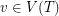$v \in V(T)$ adjacent to 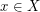$x \in X$ if and only if $v$ lies on the ray $x$ (in $G$ ). 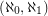Any $(\aleph_0,\aleph_1)$ -graph which is isomorphic to a subgraph of this graph is said to be of binary type.

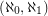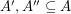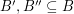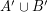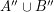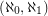Say that a $(\aleph_0,\aleph_1)$ -graph is divisible if there exist disjoint subsets $A',A'' \subseteq A$ and disjoint subsets $B',B'' \subseteq B$ so that the graphs induced by both $A' \cup B'$ and $A'' \cup B''$ are $(\aleph_0,\aleph_1)$ -graphs. It is not difficult to show that every binary type graph is divisible. Curiously, the existence of non-divisible 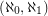$(\aleph_0,\aleph_1)$ -graphs depends on the Continuum Hypothesis (see [DL]).

Although it is not clear wether or not there is a nice characterization of 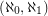$(\aleph_0,\aleph_1)$ -graphs, it would certainly be interesting to find more natural families of these graphs. The following rather more concrete question is posed by Diestel and Leader who suspect the answer is 'no'.

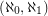Problem Does every $(\aleph_0,\aleph_1)$ -graph have an 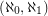$(\aleph_0,\aleph_1)$ -graph as a minor which is either indivisible or of binary type?

Bibliography

[DL] R. Diestel and I. Leader, Normal spanning trees, Aronszajn trees and excluded minors, J. London Math. Soc. 63 (2001), 16-32;

* indicates original appearance(s) of problem.

2 comments

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity