 login/create account
login/create account
If 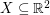 is a finite set of points which is 2-colored, an empty triangle is a set
is a finite set of points which is 2-colored, an empty triangle is a set 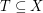 with
with 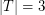 so that the convex hull of
so that the convex hull of  is disjoint from
is disjoint from  . We say that
. We say that  is monochromatic if all points in
is monochromatic if all points in  are the same color.
are the same color.
Conjecture There exists a fixed constant  with the following property. If
with the following property. If 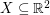 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 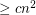 monochromatic empty triangles.
monochromatic empty triangles.
 with the following property. If
with the following property. If 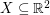 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 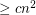 monochromatic empty triangles.
monochromatic empty triangles. It is known that any set of  points in the plane in general position contains
points in the plane in general position contains 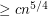 monochromatic empty triangles.
monochromatic empty triangles.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University