Home » Subject » Theoretical Comp. Sci. » Algorithms
Importance: Medium ✭✭
Author(s): Lipton, Dick
Subject: Theoretical Computer Science
» Algorithms
Keywords: Algorithm construction
Exponential-time algorithm
Knapsack
Recomm. for undergrads: yes
Posted by: dick lipton
on: February 4th, 2009
Conjecture  

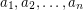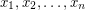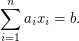The famous 0-1 Knapsack problem is: Given $ a_{1},a_{2},\dots,a_{n} $ and $ b $ integers, determine whether or not there are $ 0-1 $ values $ x_{1},x_{2},\dots,x_{n} $ so that $$ \sum_{i=1}^{n} a_{i}x_{i} = b.$$ The best known worst-case algorithm runs in time $ 2^{n/2} $ times a polynomial in $ n $. Is there an algorithm that runs in time $ 2^{n/3} $?


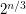Bibliography

[SS] Richard Schroeppel and Adi Shamir. A T=O(2n/2), S=O(2n/4) algorithm for certain NP-complete problems, SIAM J. Comput. 10 (1981), no. 3, 456--464.


* indicates original appearance(s) of problem.
7 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options