 login/create account
login/create account
Conjecture Let 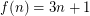 if
if  is odd and
is odd and 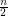 if
if  is even. Let
is even. Let 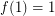 . Assume we start with some number
. Assume we start with some number  and repeatedly take the
and repeatedly take the  of the current number. Prove that no matter what the initial number is we eventually reach
of the current number. Prove that no matter what the initial number is we eventually reach 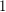 .
.
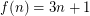 if
if  is odd and
is odd and 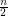 if
if  is even. Let
is even. Let 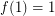 . Assume we start with some number
. Assume we start with some number  and repeatedly take the
and repeatedly take the  of the current number. Prove that no matter what the initial number is we eventually reach
of the current number. Prove that no matter what the initial number is we eventually reach 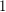 .
. This problem is also called Collatz conjecture, Ulam conjecture, or the Syracuse problem. For a more extensive discussion, visit the wikipedia article or [L].
Bibliography
[L] Jeffrey C. Lagarias: The 3x+1 problem: An annotated bibliography (1963--2000)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University