 login/create account
login/create account
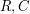 , their Tensor Product
, their Tensor Product 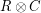 is the code that consists of the matrices whose rows are codewords of
is the code that consists of the matrices whose rows are codewords of 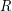 and whose columns are codewords of
and whose columns are codewords of 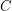 . The product
. The product 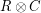 is said to be robust if whenever a matrix
is said to be robust if whenever a matrix 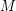 is far from
is far from 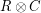 , the rows (columns) of
, the rows (columns) of 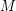 are far from
are far from 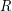 (
(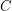 , respectively).
, respectively).
The problem is to give a characterization of the pairs 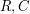 whose tensor product is robust.
whose tensor product is robust.
The question is studied in the context of Locally Testable Codes.
Bibliography
*[BS] Eli Ben-Sasson, Madhu Sudan, Robust locally testable codes and products of codes, APPROX-RANDOM 2004, pp. 286-297 (See ECCC TR04-046).
[CR] D. Coppersmith and A. Rudra, On the robust testability of tensor products of codes, ECCC TR07-061.
[DSW] Irit Dinur, Madhu Sudan and Avi Wigderson, Robust local testability of tensor products of LDPC codes, APPROX-RANDOM 2006, pp. 304-315 (See ECCC TR06-118).
[GM] Oded Goldreich, Or Meir, The Tensor Product of Two Good Codes Is Not Necessarily Robustly Testable, ECCC TR07-062.
[M] Or Meir, On the Rectangle Method in proofs of Robustness of Tensor Products, ECCC TR07-061.
[V] Paul Valiant, The Tensor Product of Two Codes Is Not Necessarily Robustly Testable, APPROX-RANDOM 2005, pp. 472-481.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University