 login/create account
login/create account
Conjecture Every odd number coprime to its Euler totient divides some Carmichael Number.
In December 2007 Joe Crump discovered the following Carmichael multiples (of the numbers with previously unknown Carmichael multiples):
- \item
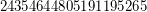 is a Carmichael multiple of
is a Carmichael multiple of 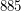 ; \item
; \item 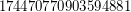 is a Carmichael multiple of
is a Carmichael multiple of 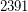 ; \item
; \item 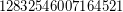 is a Carmichael multiple of
is a Carmichael multiple of 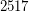 ; \item
; \item 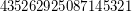 is a Carmichael multiple of
is a Carmichael multiple of  ; \item
; \item 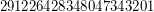 is a Carmichael multiple of
is a Carmichael multiple of 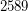 ; \item
; \item 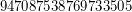 is a Carmichael multiple of
is a Carmichael multiple of 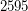 ; \item
; \item 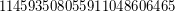 is a Carmichael multiple of
is a Carmichael multiple of 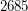 ; \item
; \item 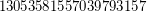 is a Carmichael multiple of
is a Carmichael multiple of 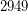 .
. Bibliography
Gérard P. Michon. "Least Carmichael Numbers with Given Divisors (up to 2999)."
Gérard P. Michon and Joseph K. Crump. "Carmichael Multiples of Odd Cyclic Numbers."
W. R. Alford, A. Granville, and C. Pomerance. "There are Infinitely Many Carmichael Numbers." Ann. Math. 139, 703-722, 1994.
Günter Löh and Wolfgang Niebuhr. "A new algorithm for constructing large Carmichael numbers." Math. Comp. 65 (1996), 823-836.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University