Home » Subject » Graph Theory » Basic G.T.
Importance: High ✭✭✭
Author(s): Adel P. Kazemi
Subject: Graph Theory
» Basic Graph Theory
Keywords: Total domination number, Hypercube
Recomm. for undergrads: no
Posted by: Adel P. Kazemi
on: October 6th, 2013
Solved by: See comment.
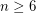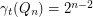Conjecture   For any integer $ n\geq 6 $, $ \gamma_t(Q_n) = 2^{n-2} $.

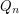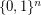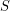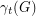Here $ Q_n $ denotes the $ n $-dimensional hypercube, i.e. the graph with vertex set $ \{0,1\}^n $ and two vertices adjacent if they differ in exactly one coordinate. A total dominating set of a graph $ G $ is a set $ S $ of vertices of $ G $ such that every vertex has at least one neighbor in $ S $". The total domination number $ \gamma_t(G) $ of $ G $ is the cardinality of a minimum total dominating set. 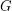A total dominator coloring of a graph $ G $, briefly TDC, is a proper coloring of 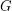$ G $ in which each vertex of the graph is adjacent to every vertex of some color class. 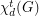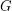The total dominator chromatic number $ \chi_d^t(G) $ of $ G $ is the minimum number of color classes in a TDC in 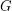$ G $ (see [Kaz1]).

The following theorems are proved in [Kaz2].

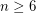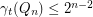Theorem   For any integer $ n\geq 6 $, $ \gamma_t(Q_n)\leq2^{n-2} $.
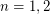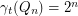Theorem   1. If $ n=1,2 $, then $ \gamma_t(Q_n)=2^n $.
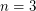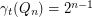2. If $ n=3 $, then $ \gamma_t(Q_n)=2^{n-1} $.
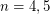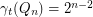3. If $ n=4,5 $, then $ \gamma_t(Q_n)=2^{n-2} $.
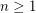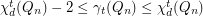Theorem   For any integer $ n\geq 1 $, $ \chi_d^t(Q_n)-2 \leq \gamma_t(Q_n) \leq \chi_d^t(Q_n) $.

Bibliography

[Kaz1] Adel P. Kazemi, Total dominator chromatic number of a graph, http://arxiv.org/abs/1307.7486.

[Kaz2] Adel P. Kazemi, Total Dominator Coloring in Product Graphs, Utilitas Mathematica (2013), Accepted.


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options