Home » Subject » Graph Theory » Basic G.T. » Cycles

Hamiltonian cycles in line graphs

Importance: High ✭✭✭
Author(s): Thomassen, Carsten
Subject: Graph Theory
» Basic Graph Theory
» » Cycles
Keywords: hamiltonian
line graphs
Recomm. for undergrads: no
Posted by: Robert Samal
on: July 24th, 2007
Conjecture   Every 4-connected line graph is hamiltonian.
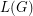    \item It is known that if $ G $ is 4-edge-connected, then its line graph $ L(G) $ is hamiltonian. \item Thomassen's is a special case of a conjecture due to Matthews and Sumner: every 4-connected claw-free graph is hamiltonian. \item However, by a result of Ryjacek [R] conjectures of Thomassen and of Matthews and Sumner are equivalent. \item Moreover [R], one may restrict to 4-connected line graphs of triangle-free graphs.

Bibliography

[R] Zdenek Ryjacek: On a closure concept in claw-free graphs. J. Combin. Theory Ser. B 70 (1997), no. 2, 217--224, MathSciNet

*[T] Carsten Thomassen, Reflections on graph theory, J. Graph Theory 10 (1986) 309-324, MathSciNet


* indicates original appearance(s) of problem.
add new comment