 login/create account
login/create account
Cross-composition product of reloids is a quasi-cartesian function
Conjecture Cross-composition product (for small indexed families of reloids) is a quasi-cartesian function (with injective aggregation) from the quasi-cartesian situation 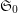 of reloids to the quasi-cartesian situation
of reloids to the quasi-cartesian situation  of pointfree funcoids over posets with least elements.
of pointfree funcoids over posets with least elements.
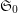 of reloids to the quasi-cartesian situation
of reloids to the quasi-cartesian situation  of pointfree funcoids over posets with least elements.
of pointfree funcoids over posets with least elements. This conjecture is unsolved even for product of two multipliers.
An obviously equivalent reformulation of this conjecture for the special case of two multipliers:
Conjecture Provided that reloids  and
and  on some set
on some set 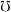 are proper filters, we can restore the values of
are proper filters, we can restore the values of  and
and  knowing only
knowing only 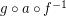 for every reloid
for every reloid  on
on 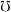 .
.
 and
and  on some set
on some set 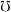 are proper filters, we can restore the values of
are proper filters, we can restore the values of  and
and  knowing only
knowing only 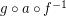 for every reloid
for every reloid  on
on 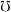 .
. Reloids are defined simply as filters on a Cartesian product of two sets. The reverse reloid 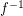 of a reloids
of a reloids  is defined by the formula:
is defined by the formula:  . Composition
. Composition 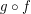 of reloids
of reloids  and
and  is defined as the reloid whose base is
is defined as the reloid whose base is 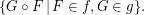
See Algebraic General Topology for definitions of used concepts.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University