 login/create account
login/create account
addition table
Snevily's conjecture ★★★
Author(s): Snevily
Conjecture Let  be an abelian group of odd order and let
be an abelian group of odd order and let 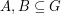 satisfy
satisfy 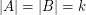 . Then the elements of
. Then the elements of  and
and 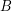 may be ordered
may be ordered 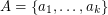 and
and 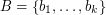 so that the sums
so that the sums 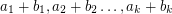 are pairwise distinct.
are pairwise distinct.
 be an abelian group of odd order and let
be an abelian group of odd order and let 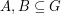 satisfy
satisfy 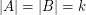 . Then the elements of
. Then the elements of  and
and 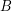 may be ordered
may be ordered 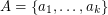 and
and 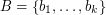 so that the sums
so that the sums 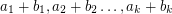 are pairwise distinct.
are pairwise distinct. Keywords: addition table; latin square; transversal

 Drupal
Drupal CSI of Charles University
CSI of Charles University