 login/create account
login/create account
Fowler, Patrick W.
Fowler's Conjecture on eigenvalues of (3,6)-polyhedra ★★
Author(s): Fowler
Conjecture Let  be the graph of a
be the graph of a 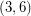 -polyhedron with
-polyhedron with 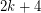 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 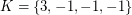 ,
, 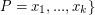 (where
(where 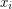 is nonnegative for
is nonnegative for 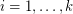 ), and
), and 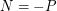 .
.
 be the graph of a
be the graph of a 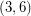 -polyhedron with
-polyhedron with 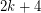 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 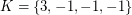 ,
, 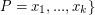 (where
(where 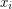 is nonnegative for
is nonnegative for 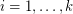 ), and
), and 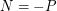 .
. Keywords: (3,6)-polyhedron; eigenvalues

 Drupal
Drupal CSI of Charles University
CSI of Charles University