 login/create account
login/create account
Hurtado, Ferran
Chromatic number of associahedron ★★
Author(s): Fabila-Monroy; Flores-Penaloza; Huemer; Hurtado; Urrutia; Wood
Conjecture Associahedra have unbounded chromatic number.
Edge-Colouring Geometric Complete Graphs ★★
Author(s): Hurtado
Question What is the minimum number of colours such that every complete geometric graph on  vertices has an edge colouring such that:
vertices has an edge colouring such that:
 vertices has an edge colouring such that:
vertices has an edge colouring such that:- \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.
Keywords: geometric complete graph, colouring
3-Colourability of Arrangements of Great Circles ★★
Author(s): Felsner; Hurtado; Noy; Streinu
Consider a set  of great circles on a sphere with no three circles meeting at a point. The arrangement graph of
of great circles on a sphere with no three circles meeting at a point. The arrangement graph of  has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
Conjecture Every arrangement graph of a set of great circles is 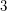 -colourable.
-colourable.
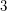 -colourable.
-colourable. Keywords: arrangement graph; graph coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University