 login/create account
login/create account
primality
Alexa's Conjecture on Primality ★★
Author(s): Alexa
Definition Let 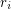 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 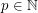 ) such that
) such that
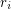 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 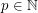 ) such that
) such that
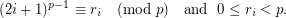
Conjecture A natural number 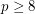 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
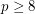 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
Keywords: primality
Giuga's Conjecture on Primality ★★
Author(s): Giuseppe Giuga
Conjecture 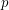 is a prime iff
is a prime iff 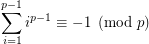
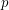 is a prime iff
is a prime iff 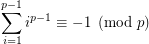
Keywords: primality
MacEachen Conjecture ★
Author(s): McEachen
Conjecture Every odd prime number must either be adjacent to, or a prime distance away from a primorial or primorial product.
Keywords: primality; prime distribution

 Drupal
Drupal CSI of Charles University
CSI of Charles University