 login/create account
login/create account
prime
Sum of prime and semiprime conjecture ★★
Author(s): Geoffrey Marnell
Conjecture Every even number greater than 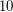 can be represented as the sum of an odd prime number and an odd semiprime .
can be represented as the sum of an odd prime number and an odd semiprime .
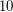 can be represented as the sum of an odd prime number and an odd semiprime .
can be represented as the sum of an odd prime number and an odd semiprime . Polignac's Conjecture ★★★
Author(s): de Polignac
Conjecture Polignac's Conjecture: For any positive even number n, there are infinitely many prime gaps of size n. In other words: There are infinitely many cases of two consecutive prime numbers with difference n.
In particular, this implies:
Conjecture Twin Prime Conjecture: There are an infinite number of twin primes.
Are there an infinite number of lucky primes? ★
Author(s): Lazarus: Gardiner: Metropolis; Ulam
Conjecture If every second positive integer except 2 is remaining, then every third remaining integer except 3, then every fourth remaining integer etc. , an infinite number of the remaining integers are prime.
Twin prime conjecture ★★★★
Author(s):
Conjecture There exist infinitely many positive integers  so that both
so that both  and
and 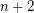 are prime.
are prime.
 so that both
so that both  and
and 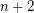 are prime.
are prime.
Keywords: prime; twin prime
Wall-Sun-Sun primes and Fibonacci divisibility ★★
Author(s):
Conjecture For any prime 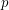 , there exists a Fibonacci number divisible by
, there exists a Fibonacci number divisible by 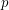 exactly once.
exactly once.
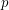 , there exists a Fibonacci number divisible by
, there exists a Fibonacci number divisible by 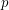 exactly once.
exactly once. Equivalently:
Conjecture For any prime 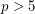 ,
, 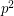 does not divide
does not divide  where
where 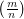 is the Legendre symbol.
is the Legendre symbol.
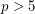 ,
, 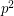 does not divide
does not divide  where
where 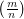 is the Legendre symbol.
is the Legendre symbol. Goldbach conjecture ★★★★
Author(s): Goldbach
Conjecture Every even integer greater than 2 is the sum of two primes.
Keywords: additive basis; prime

 Drupal
Drupal CSI of Charles University
CSI of Charles University