 login/create account
login/create account
reverse mathematics
Distributivity of a lattice of funcoids is not provable without axiom of choice ★
Author(s): Porton
Conjecture Distributivity of the lattice 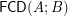 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets 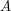 and
and 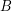 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice).
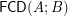 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets 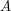 and
and 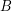 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
Conjecture 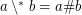 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice).
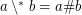 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). Keywords: axiom of choice; distributive lattice; distributivity; funcoid; reverse math; reverse mathematics; ZF; ZFC

 Drupal
Drupal CSI of Charles University
CSI of Charles University