I like thinking about this problem in terms of fractional colourings. A roughly equivalent proof (to the one you mentioned) is as follows. In a fractional 3-edge-colouring, every matching must be a perfect matching. The weights on the matchings, when divided by 3, give you a probability distribution. If you pick matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of of one another.
Here are two even weaker questions:
Is there some such that any bridgeless cubic graph contains perfect matchings whose intersection does not contain an odd cut?
Does every bridgeless cubic graph contain two perfect matchings that together hit no 5-cut 8 or 10 times?
Matchings and odd cuts
I like thinking about this problem in terms of fractional colourings. A roughly equivalent proof (to the one you mentioned) is as follows. In a fractional 3-edge-colouring, every matching must be a perfect matching. The weights on the matchings, when divided by 3, give you a probability distribution. If you pick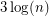 matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of
matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of  of one another.
of one another.
Here are two even weaker questions:
Is there some such that any bridgeless cubic graph contains
such that any bridgeless cubic graph contains  perfect matchings whose intersection does not contain an odd cut?
perfect matchings whose intersection does not contain an odd cut?
Does every bridgeless cubic graph contain two perfect matchings that together hit no 5-cut 8 or 10 times?
I suspect both of these are open as well.