Once again, the paper cited offers only a partial solution. Quoting from the paper, "From Theorem 1.1, we conclude that the strong chromatic number can be bounded by if . This result should not be compared with the more complete and difficult result of Alon." Here, the difficult result of Alon is the theorem that there exists a fixed constant so that every graph of maximum degree is strongly -colorable.. precisely the result which is sharpened by this conjecture.
login/create account
Drupal
CSI of Charles University
still only a partial solution
Once again, the paper cited offers only a partial solution. Quoting from the paper, "From Theorem 1.1, we conclude that the strong chromatic number can be bounded by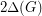
if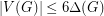 
. This result should not be compared with the more complete and difficult result of Alon." Here, the difficult result of Alon is the theorem that there exists a fixed constant 
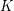so that every graph of maximum degree 
is strongly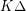 
-colorable.. precisely the result which is sharpened by this conjecture.