Home » Subject » Geometry
Importance: High ✭✭✭
Author(s): Ulam, Stanislaw M.
Subject: Geometry
Keywords: integral distance
rational distance
Recomm. for undergrads: no
Posted by: mdevos
on: July 4th, 2008
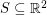Problem   Does there exist a dense set $ S \subseteq {\mathbb R}^2 $ so that all pairwise distances between points in $ S $ are rational?

This famous problem was asked by Ulam, who guessed the answer would be negative.

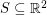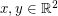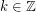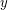A cute theorem of Erdos shows that if $ S \subseteq {\mathbb R}^2 $ is non-collinear and all pairwise distances between points in $ S $ are integral, then $ S $ is finite. 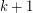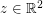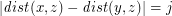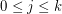For the proof, first note that if $ x,y \in {\mathbb R}^2 $ have distance $ k \in {\mathbb Z} $, then every point which has integer distance to both $ x $ and $ y $ must lie on one of the $ k+1 $ hyperbolas consisting of those $ z \in {\mathbb R}^2 $ with $ |{\mathit dist}(x,z) - {\mathit dist}(y,z)| = j $ for some $ 0 \le j \le k $. 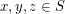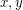So, if all pairwise distances between points in $ S $ are integral, and $ x,y,z \in S $ are non-collinear, then every other point in $ S $ must lie on an intersection between one of finitely many hyperbola with foci $ x,y $ and one of finitely many with foci 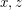$ x,z $. This set is necessarily finite, thus completing the proof.

Of course, the above argument gives no upper bound on the size of a non-collinear set of points in 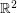$ {\mathbb R}^2 $ with pairwise integral distances. Indeed, if Ulam's conjecture is true, then there exist such sets of arbitrary size. Surprisingly, it is very difficult to construct such sets $ S $ of even rather small size. Recently Kreisel and Kurz [KK] found such a set of size 7, but it is unknown if there exists one of size 8.

It is trivial to find infinitely many points on a line with all pairwise distances rational. Less trivially, there exist infinite subsets of a circle with all pairwise distances rational. Very recently, Solymosi and De Zeeuw [SZ] proved that these are the only two irreducible algebraic curves with this property. This suggests that, if the answer to Ulam's problem is affirmative, such a set $ S $ must be extremely special.

Bibliography

[KK] T. Kreisel and S. Kurz, There are integral heptagons, no three points on a line, no four on a circle, Discrete & Computational Geometry, Online first: DOI 10.1007/s00454-007-9038-6

[SZ] J. Solymosi and F. de Zeeuw, On a question of Erdos and Ulam.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options