Home » Subject » Geometry » Algebraic Geometry
Importance: Outstanding ✭✭✭✭
Author(s): Hodge, W. V. D.
Subject: Geometry
» Algebraic Geometry
Keywords: Hodge Theory
Millenium Problems
Recomm. for undergrads: no
Prize: $1,000,000 from the Clay Mathematics Institute
Posted by: Charles
on: July 13th, 2008
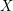Conjecture   Let $ X $ be a complex projective variety. Then every Hodge class is a rational linear combination of the cohomology classes of complex subvarieties of $ X $.

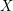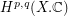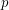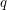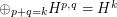A complex projective variety is the set of zeros of a finite collection of homogeneous polynomials on projective space, and we are concerned with the singular cohomology ring. There is a well known Hodge Decomposition of the cohomology into groups $ H^{p,q}(X.\mathbb{C}) $ which hare holomorphic in $ p $ variables and antiholomorphic in $ q $ variables with the property that $ \oplus_{p+q=k}H^{p,q}=H^k $.

So we define the Hodge classes to be those in the intersection 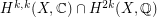$ H^{k,k}(X,\mathbb{C})\cap H^{2k}(X,\mathbb{Q}) $. It is fairly easy to show that the cohomology class of a subvariety is Hodge. We say that a cycle is algebraic if it is a rational linear combination of the classes of subvarieties. So every algebraic cycle is Hodge. In dimension one, we have the following result:

Theorem  (Lefshetz (1,1) Theorem)   Any element of $ H^2(X,\mathbb{Q})\cap H^{1,1} $ is the cohomology class of a divisor, and so is algebraic.

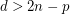It's also true that if the Hodge Conjecture holds for cycles of degree $ p<n $, then it holds for cycles of degree $ d>2n-p $. So this and the (1,1) Theorem show that the Hodge Conjecture is true for complex curves, surfaces and threefolds.

Bibliography

*[Hod] Hodge, W. V. D. "The topological invariants of algebraic varieties". Proceedings of the International Congress of Mathematicians, Cambridge, MA, 1950, vol. 1, pp. 181–192.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options