 login/create account
login/create account
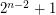 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. This is one of the most famous unsolved problems in combinatorial geometry, perhaps due in part to its lovely history. The problem of showing that every sufficiently large set of points in general position determine a convex  -gon was the original inspiration of Esther Klein. Erdös called this the Happy end problem since it led to the marriage of Esther Klein and George Szekeres. This problem was also one of the original sources of Ramsey Theory.
-gon was the original inspiration of Esther Klein. Erdös called this the Happy end problem since it led to the marriage of Esther Klein and George Szekeres. This problem was also one of the original sources of Ramsey Theory.
Let 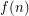 denote the smallest integer so that every set of
denote the smallest integer so that every set of 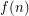 points in the plane in general position contains
points in the plane in general position contains  points which form a convex
points which form a convex  -gon. The fact that
-gon. The fact that 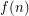 exists for every
exists for every  was first established in a seminal paper of Erdös and Szekeres who proved the following bounds on
was first established in a seminal paper of Erdös and Szekeres who proved the following bounds on 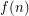 .
. ![\[ 2^{n-2} + 1 \le f(n) \le { 2n-4 \choose n-2 } + 1 \]](/files/tex/1310cd34786c87452b44d74376b43a1e75d8f2f6.png)
The lower bound is conjectured to be the truth, and this is known to hold for 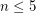 . A handful of recent papers on this problem have improved the upper bound to
. A handful of recent papers on this problem have improved the upper bound to ![\[ f(n) \le {2n-5 \choose n-3} + 1. \]](/files/tex/b6f9c646ae2fdaa2c2107e2498da075eb7848a0b.png)
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University