 login/create account
login/create account
Erdos, Paul
Multicolour Erdős--Hajnal Conjecture ★★★
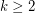 and fixed colouring
and fixed colouring 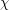 of
of 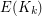 with
with  colours, there exists
colours, there exists 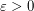 such that every colouring of the edges of
such that every colouring of the edges of 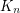 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 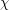 or
or 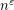 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 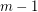 colours.
colours. Keywords: ramsey theory
Turán Problem for $10$-Cycles in the Hypercube ★★
Author(s): Erdos
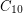 in the hypercube.
in the hypercube. Keywords: cycles; extremal combinatorics; hypercube
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
Odd-cycle transversal in triangle-free graphs ★★
Author(s): Erdos; Faudree; Pach; Spencer
 is a simple triangle-free graph, then there is a set of at most
is a simple triangle-free graph, then there is a set of at most 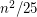 edges whose deletion destroys every odd cycle.
edges whose deletion destroys every odd cycle. Keywords:
Turán number of a finite family. ★★
Author(s): Erdos; Simonovits
Given a finite family 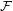 of graphs and an integer
of graphs and an integer  , the Turán number
, the Turán number 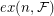 of
of 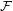 is the largest integer
is the largest integer  such that there exists a graph on
such that there exists a graph on  vertices with
vertices with  edges which contains no member of
edges which contains no member of 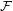 as a subgraph.
as a subgraph.
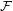 of graphs there exists an
of graphs there exists an 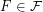 such that
such that 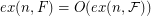 .
.
Keywords:
Strong edge colouring conjecture ★★
A strong edge-colouring of a graph  is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index
is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index 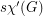 is the minimum number of colours in a strong edge-colouring of
is the minimum number of colours in a strong edge-colouring of  .
.

Keywords:
Erdős–Straus conjecture ★★
For all 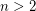 , there exist positive integers
, there exist positive integers  ,
, 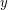 ,
,  such that
such that 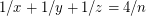 .
.
Keywords: Egyptian fraction
Double-critical graph conjecture ★★
A connected simple graph  is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
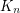 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph Keywords: coloring; complete graph
Erdös-Szekeres conjecture ★★★
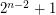 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. Keywords: combinatorial geometry; Convex Polygons; ramsey theory
Middle levels problem ★★
Author(s): Erdos
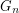 be the bipartite graph whose vertices are the
be the bipartite graph whose vertices are the  -subsets and the
-subsets and the 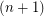 -subsets of a
-subsets of a 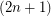 -element set, and with inclusion as the adjacency relationship. Then
-element set, and with inclusion as the adjacency relationship. Then 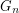 is Hamiltonian.
is Hamiltonian. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University