Home » Subject » Graph Theory

Turán number of a finite family.

Importance: Medium ✭✭
Author(s): Erdos, Paul
Simonovits, Miklos
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 5th, 2013

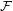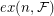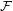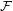Given a finite family $ {\cal F} $ of graphs and an integer $ n $, the Turán number $ ex(n,{\cal F}) $ of $ {\cal F} $ is the largest integer $ m $ such that there exists a graph on $ n $ vertices with $ m $ edges which contains no member of $ {\cal F} $ as a subgraph.

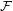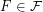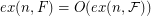Conjecture   For every finite family $ {\cal F} $ of graphs there exists an $ F\in {\cal F} $ such that $ ex(n, F ) = O(ex(n, {\cal F})) $ .

For the case when 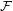$ {\cal F} $ consists of even cycles, this would mean that (up to constants) the Turán number of 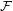$ {\cal F} $ is given by that of the longest cycle in 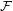$ {\cal F} $. Verstraëte (see [KO]) conjectured something stronger:

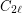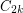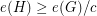Conjecture   For all integers $ k < \ell $ there exists a positive c = c(\ell) such that every $ C_{2\ell} $-free graph $ G $ has a $ C_{2k} $-free subgraph $ H $ with $ e(H) ≥ e(G)/c $.

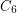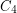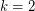This conjecture was motivated by a result of Györi [G] who showed that every bipartite $ C_6 $-free graph $ G $ has a $ C_4 $-free subgraph which contains at least half of the edges of $ G $. The case $ k=2 $ was proved in [KO].

Bibliography

*[ES] P.Erdös and M. Simonovits, Compactness results in extremal graph theory, Combinatorica 2 (1982), 275–288.

[KO] D. Kühn and D. Osthus, 4-cycles in graphs without a given even cycle, J. Graph Theory 48 (2005), 147-156.

[G] E. Györi, 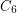$ C_6 $-free bipartite graphs and product representation of squares, Discrete Math. 165/166 (1997), 371-375.


* indicates original appearance(s) of problem.
add new comment