 login/create account
login/create account
Strong edge colouring conjecture
A strong edge-colouring of a graph  is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index
is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index 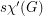 is the minimum number of colours in a strong edge-colouring of
is the minimum number of colours in a strong edge-colouring of  .
.
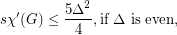
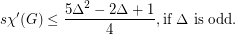
The conjectured bounds would be sharp. When 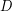 is even, expanding each vertex of a
is even, expanding each vertex of a  -cycle into a stable set of size
-cycle into a stable set of size 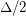 yields such a graph with
yields such a graph with 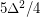 edges in which the largest induced matching has size
edges in which the largest induced matching has size 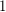 . A similar construction achieves the bound when
. A similar construction achieves the bound when  is odd.
is odd.
Greedy colouring the edges yields 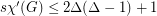 . Using probabilistic methods, Molloy and Reed~[MoRe97] proved that there is a positive constant
. Using probabilistic methods, Molloy and Reed~[MoRe97] proved that there is a positive constant  such that, for sufficiently large
such that, for sufficiently large  , every graph with maximum degree
, every graph with maximum degree  has strong chromatic index at most
has strong chromatic index at most 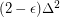 .
.
The greedy bound proves the conjecture for 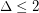 . For
. For 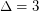 , the conjectured bound of 10 was proved independently by Hor\'ak, He, and Trotter[HHT] and by Andersen [A]. For
, the conjectured bound of 10 was proved independently by Hor\'ak, He, and Trotter[HHT] and by Andersen [A]. For 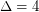 , the conjectured bound is 20, and Cranston [C] proved that 22 colours suffice.
, the conjectured bound is 20, and Cranston [C] proved that 22 colours suffice.
For a bipartite graph  , Faudree et al. [FGST] conjectured that
, Faudree et al. [FGST] conjectured that 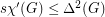 . This is implied by the stronger conjecture due to Kaiser.
. This is implied by the stronger conjecture due to Kaiser.
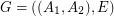 be a bipartite graph such that every vertex in
be a bipartite graph such that every vertex in 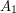 has degree at most
has degree at most 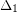 and every vertex in
and every vertex in 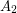 has degree at most
has degree at most 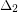 . Then
. Then 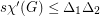 .
. Bibliography
[A] L. D. Andersen. The strong chromatic index of a cubic graph is at most 10. Discrete Math., 108(1-3):231--252, 1992.
[C] D. W. Cranston. Strong edge-coloring of graphs with maximum degree 4 using 22 colors. Discrete Math., 306(21):2772--2778, 2006.
[FGST] R. J. Faudree, A. Gyárfás, R. H. Schelp, and Zs. Tuza. Induced matchings in bipartite graphs. Discrete Math., 78(1-2):83--87, 1989.
[HHT] P. Horák, Q. He, and W. T. Trotter. Induced matchings in cubic graphs. J. Graph Theory, 17(2):151--160, 1993.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University