 login/create account
login/create account
Nesetril, Jaroslav
Strong edge colouring conjecture ★★
A strong edge-colouring of a graph  is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index
is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index 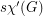 is the minimum number of colours in a strong edge-colouring of
is the minimum number of colours in a strong edge-colouring of  .
.
Conjecture 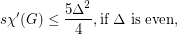


Keywords:
Long rainbow arithmetic progressions ★★
Author(s): Fox; Jungic; Mahdian; Nesetril; Radoicic
For 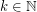 let
let 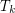 denote the minimal number
denote the minimal number 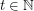 such that there is a rainbow
such that there is a rainbow 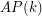 in every equinumerous
in every equinumerous 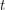 -coloring of
-coloring of 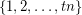 for every
for every 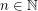
Conjecture For all  ,
, 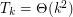 .
.
 ,
, 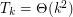 .
. Keywords: arithmetic progression; rainbow
Pentagon problem ★★★
Author(s): Nesetril
Question Let  be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism  ?
?
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism  ?
? Keywords: cubic; homomorphism

 Drupal
Drupal CSI of Charles University
CSI of Charles University