Home » Subject » Graph Theory » Coloring

Vertex coloring


Graph Theory » Coloring » Vertex coloring

Strong colorability ★★★

Author(s): Aharoni; Alon; Haxell

Let $ r $ be a positive integer. We say that a graph $ G $ is strongly $ r $-colorable if for every partition of the vertices to sets of size at most $ r $ there is a proper $ r $-coloring of $ G $ in which the vertices in each set of the partition have distinct colors.

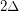Conjecture   If $ \Delta $ is the maximal degree of a graph $ G $, then $ G $ is strongly $ 2 \Delta $-colorable.

Keywords: strong coloring

Posted by berger
updated November 19th, 2009
5 comments
Graph Theory » Coloring » Vertex coloring

Reed's omega, delta, and chi conjecture ★★★

Author(s): Reed

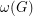For a graph $ G $, we define $ \Delta(G) $ to be the maximum degree, $ \omega(G) $ to be the size of the largest clique subgraph, and 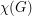$ \chi(G) $ to be the chromatic number of $ G $.

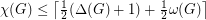Conjecture   $ \chi(G) \le \ceil{\frac{1}{2}(\Delta(G)+1) + \frac{1}{2}\omega(G)} $ for every graph $ G $.

Keywords: coloring

Posted by mdevos
updated September 24th, 2007
2 comments
Graph Theory » Coloring » Vertex coloring

Circular coloring triangle-free subcubic planar graphs ★★

Author(s): Ghebleh; Zhu

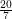Problem   Does every triangle-free planar graph of maximum degree three have circular chromatic number at most $ \frac{20}{7} $?

Keywords: circular coloring; planar graph; triangle free

Posted by mdevos
updated June 20th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Oriented chromatic number of planar graphs ★★

Author(s):

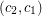An oriented colouring of an oriented graph is assignment $ c $ of colours to the vertices such that no two arcs receive ordered pairs of colours $ (c_1,c_2) $ and $ (c_2,c_1) $. It is equivalent to a homomorphism of the digraph onto some tournament of order $ k $.

Problem   What is the maximal possible oriented chromatic number of an oriented planar graph?

Keywords: oriented coloring; oriented graph; planar graph

Posted by Robert Samal
updated August 4th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Coloring and immersion ★★★

Author(s): Abu-Khzam; Langston

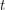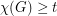Conjecture   For every positive integer $ t $, every (loopless) graph $ G $ with $ \chi(G) \ge t $ immerses $ K_t $.

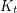Keywords: coloring; complete graph; immersion

Posted by mdevos
updated September 4th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Coloring the Odd Distance Graph ★★★

Author(s): Rosenfeld

The Odd Distance Graph, denoted 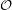$ {\mathcal O} $, is the graph with vertex set 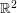$ {\mathbb R}^2 $ and two points adjacent if the distance between them is an odd integer.

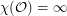Question   Is $ \chi({\mathcal O}) = \infty $?

Keywords: coloring; geometric graph; odd distance

Posted by mdevos
updated March 19th, 2012
8 comments
Graph Theory » Coloring » Vertex coloring

Partial List Coloring ★★★

Author(s): Albertson; Grossman; Haas

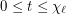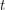Conjecture   Let $ G $ be a simple graph with $ n $ vertices and list chromatic number $ \chi_\ell(G) $. Suppose that $ 0\leq t\leq \chi_\ell $ and each vertex of $ G $ is assigned a list of $ t $ colors. Then at least 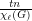$ \frac{tn}{\chi_\ell(G)} $ vertices of $ G $ can be colored from these lists.

Keywords: list assignment; list coloring

Posted by Iradmusa
updated May 5th, 2008
add new comment
Graph Theory » Coloring » Vertex coloring

Partial List Coloring ★★★

Author(s): Iradmusa

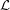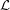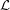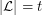Let $ G $ be a simple graph, and for every list assignment $ \mathcal{L} $ let $ \lambda_{\mathcal{L}} $ be the maximum number of vertices of $ G $ which are colorable with respect to $ \mathcal{L} $. Define $ \lambda_t = \min{ \lambda_{\mathcal{L}} } $, where the minimum is taken over all list assignments $ \mathcal{L} $ with $ |\mathcal{L}| = t $ for all $ v \in V(G) $.

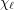Conjecture   [2] Let $ G $ be a graph with list chromatic number $ \chi_\ell $ and $ 1\leq r\leq s\leq \chi_\ell $. Then \[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]

Keywords: list assignment; list coloring

Posted by Iradmusa
updated May 12th, 2008
add new comment
Graph Theory » Coloring » Vertex coloring

Hedetniemi's Conjecture ★★★

Author(s): Hedetniemi

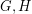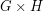Conjecture   If $ G,H $ are simple finite graphs, then $ \chi(G \times H) = \min \{ \chi(G), \chi(H) \} $.

Here $ G \times H $ is the tensor product (also called the direct or categorical product) of $ G $ and $ H $.

Keywords: categorical product; coloring; homomorphism; tensor product

Posted by mdevos
updated March 1st, 2020
5 comments
Graph Theory » Coloring » Vertex coloring

Counting 3-colorings of the hex lattice ★★

Author(s): Thomassen

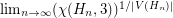Problem   Find $ \lim_{n \rightarrow \infty} (\chi( H_n , 3)) ^{ 1 / |V(H_n)| } $.

Keywords: coloring; Lieb's Ice Constant; tiling; torus

Posted by mdevos
updated July 5th, 2008
add new comment
Graph Theory » Coloring » Vertex coloring

Circular colouring the orthogonality graph ★★

Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr

Let 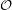$ {\mathcal O} $ denote the graph with vertex set consisting of all lines through the origin in 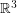$ {\mathbb R}^3 $ and two vertices adjacent in 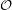$ {\mathcal O} $ if they are perpendicular.

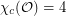Problem   Is $ \chi_c({\mathcal O}) = 4 $?

Keywords: circular coloring; geometric graph; orthogonality

Posted by mdevos
updated September 28th, 2009
4 comments
Graph Theory » Coloring » Vertex coloring

Double-critical graph conjecture ★★

Author(s): Erdos; Lovasz

A connected simple graph $ G $ is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.

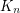Conjecture   $ K_n $ is the only $ n $-chromatic double-critical graph

Keywords: coloring; complete graph

Posted by DFR
updated November 30th, 2009
2 comments
Graph Theory » Coloring » Vertex coloring

Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★

Author(s): Kostochka; Reed

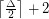Conjecture   A triangle-free graph with maximum degree $ \Delta $ has chromatic number at most $ \ceil{\frac{\Delta}{2}}+2 $.

Keywords: chromatic number; girth; maximum degree; triangle free

Posted by Andrew King
updated May 16th, 2020
1 comment
Graph Theory » Coloring » Vertex coloring

Graphs with a forbidden induced tree are chi-bounded ★★★

Author(s): Gyarfas

Say that a family 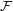$ {\mathcal F} $ of graphs is 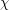$ \chi $-bounded if there exists a function 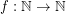$ f: {\mathbb N} \rightarrow {\mathbb N} $ so that every 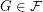$ G \in {\mathcal F} $ satisfies $ \chi(G) \le f (\omega(G)) $.

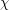Conjecture   For every fixed tree $ T $, the family of graphs with no induced subgraph isomorphic to $ T $ is $ \chi $-bounded.

Keywords: chi-bounded; coloring; excluded subgraph; tree

Posted by mdevos
updated May 16th, 2009
add new comment
Graph Theory » Coloring » Vertex coloring

Are vertex minor closed classes chi-bounded? ★★

Author(s): Geelen

Question   Is every proper vertex-minor closed class of graphs chi-bounded?

Keywords: chi-bounded; circle graph; coloring; vertex minor

Posted by mdevos
updated May 16th, 2009
add new comment
Graph Theory » Coloring » Vertex coloring

Mixing Circular Colourings ★

Author(s): Brewster; Noel

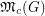Question   Is $ \mathfrak{M}_c(G) $ always rational?

Keywords: discrete homotopy; graph colourings; mixing

Posted by Jon Noel
updated September 22nd, 2012
add new comment
Graph Theory » Coloring » Vertex coloring

Choice Number of k-Chromatic Graphs of Bounded Order ★★

Author(s): Noel

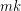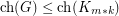Conjecture   If $ G $ is a $ k $-chromatic graph on at most $ mk $ vertices, then $ \text{ch}(G)\leq \text{ch}(K_{m*k}) $.

Keywords: choosability; complete multipartite graph; list coloring

Posted by Jon Noel
updated February 2nd, 2013
add new comment
Graph Theory » Coloring » Vertex coloring

Melnikov's valency-variety problem ★

Author(s): Melnikov

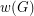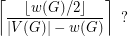
Problem   The valency-variety $ w(G) $ of a graph $ G $ is the number of different degrees in $ G $. Is the chromatic number of any graph $ G $ with at least two vertices greater than $$\ceil{ \frac{\floor{w(G)/2}}{|V(G)| - w(G)} } ~ ?$$

Keywords:

Posted by asp
updated March 3rd, 2013
add new comment
Graph Theory » Coloring » Vertex coloring

Earth-Moon Problem ★★

Author(s): Ringel

Problem   What is the maximum number of colours needed to colour countries such that no two countries sharing a common border have the same colour in the case where each country consists of one region on earth and one region on the moon ?

Keywords:

Posted by fhavet
updated March 6th, 2013
add new comment
Graph Theory » Coloring » Vertex coloring

Acyclic list colouring of planar graphs. ★★★

Author(s): Borodin; Fon-Der-Flasss; Kostochka; Raspaud; Sopena

Conjecture   Every planar graph is acyclically 5-choosable.

Keywords:

Posted by fhavet
updated March 7th, 2013
add new comment

Note: Resolved problems from this section may be found in Solved problems.


Syndicate content