 login/create account
login/create account
Mohar, Bojan
List Hadwiger Conjecture ★★
Author(s): Kawarabayashi; Mohar
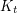 -minor-free graph is
-minor-free graph is 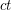 -list-colourable for some constant
-list-colourable for some constant 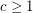 .
. Keywords: Hadwiger conjecture; list colouring; minors
Circular choosability of planar graphs ★
Author(s): Mohar
Let 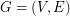 be a graph. If
be a graph. If 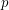 and
and 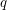 are two integers, a
are two integers, a 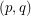 -colouring of
-colouring of  is a function
is a function  from
from 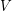 to
to 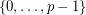 such that
such that 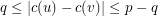 for each edge
for each edge 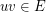 . Given a list assignment
. Given a list assignment  of
of  , i.e.~a mapping that assigns to every vertex
, i.e.~a mapping that assigns to every vertex  a set of non-negative integers, an
a set of non-negative integers, an  -colouring of
-colouring of  is a mapping
is a mapping 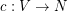 such that
such that 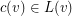 for every
for every 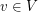 . A list assignment
. A list assignment  is a
is a 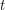 -
-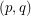 -list-assignment if
-list-assignment if 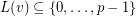 and
and 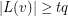 for each vertex
for each vertex 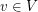 . Given such a list assignment
. Given such a list assignment  , the graph G is
, the graph G is 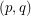 -
- -colourable if there exists a
-colourable if there exists a 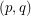 -
- -colouring
-colouring  , i.e.
, i.e.  is both a
is both a 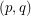 -colouring and an
-colouring and an  -colouring. For any real number
-colouring. For any real number 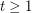 , the graph
, the graph  is
is 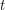 -
-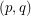 -choosable if it is
-choosable if it is 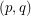 -
- -colourable for every
-colourable for every 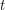 -
-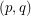 -list-assignment
-list-assignment  . Last,
. Last,  is circularly
is circularly 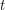 -choosable if it is
-choosable if it is 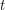 -
-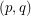 -choosable for any
-choosable for any 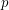 ,
, 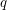 . The circular choosability (or circular list chromatic number or circular choice number) of G is
. The circular choosability (or circular list chromatic number or circular choice number) of G is 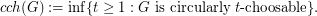
Keywords: choosability; circular colouring; planar graphs
Star chromatic index of complete graphs ★★
Author(s): Dvorak; Mohar; Samal
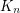 using
using 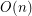 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of 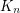 linear in
linear in  ?
?
Keywords: complete graph; edge coloring; star coloring
Star chromatic index of cubic graphs ★★
Author(s): Dvorak; Mohar; Samal
The star chromatic index 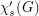 of a graph
of a graph  is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
 , we have
, we have 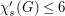 ?
? Keywords: edge coloring; star coloring
Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let 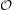 denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 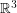 and two vertices adjacent in
and two vertices adjacent in 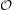 if they are perpendicular.
if they are perpendicular.
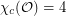 ?
? Keywords: circular coloring; geometric graph; orthogonality
Infinite uniquely hamiltonian graphs ★★
Author(s): Mohar
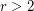 ?
? Keywords: hamiltonian; infinite graph; uniquely hamiltonian
List colorings of edge-critical graphs ★★
Author(s): Mohar
 is a
is a  -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 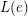 of
of  colors. Then
colors. Then  is
is  -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other. Keywords: edge-coloring; list coloring
Half-integral flow polynomial values ★★
Author(s): Mohar
Let 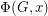 be the flow polynomial of a graph
be the flow polynomial of a graph  . So for every positive integer
. So for every positive integer  , the value
, the value 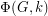 equals the number of nowhere-zero
equals the number of nowhere-zero  -flows in
-flows in  .
.
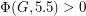 for every 2-edge-connected graph
for every 2-edge-connected graph  .
. Keywords: nowhere-zero flow
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 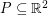 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in 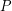 , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
 -universal set of size
-universal set of size 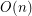 ?
? Keywords: geometric graph; planar graph; universal set
Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
 be the disjoint union of the graphs
be the disjoint union of the graphs 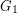 and
and 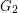 and let
and let 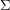 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 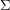 has the property that
has the property that 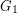 and
and 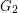 are disjoint?
are disjoint? Keywords: crossing number; surface

 Drupal
Drupal CSI of Charles University
CSI of Charles University