 login/create account
login/create account
Half-integral flow polynomial values
Let 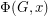 be the flow polynomial of a graph
be the flow polynomial of a graph  . So for every positive integer
. So for every positive integer  , the value
, the value 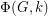 equals the number of nowhere-zero
equals the number of nowhere-zero  -flows in
-flows in  .
.
Conjecture 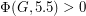 for every 2-edge-connected graph
for every 2-edge-connected graph  .
.
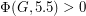 for every 2-edge-connected graph
for every 2-edge-connected graph  .
. By Seymour's 6-flow theorem, 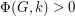 for every 2-edge-connected graph
for every 2-edge-connected graph  and every integer
and every integer 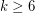 .
.
It would be interesting to find any non-integer rational number 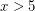 so that
so that 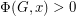 for every 2-edge-connected graph
for every 2-edge-connected graph  . It is known that zeros of flow polynomials are dense in the complex plane.
. It is known that zeros of flow polynomials are dense in the complex plane.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University