Home » Subject » Graph Theory » Topological G.T. » Drawings
Importance: High ✭✭✭
Author(s): Mohar, Bojan
Subject: Graph Theory
» Topological Graph Theory
» » Drawings
Keywords: geometric graph
planar graph
universal set
Recomm. for undergrads: no
Posted by: mdevos
on: May 22nd, 2007

We say that a set 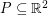$ P \subseteq {\mathbb R}^2 $ is $ n $-universal if every $ n $ vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in 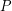$ P $, and all edges are (non-intersecting) straight line segments.

Question   Does there exist an $ n $-universal set of size $ O(n) $?

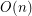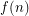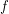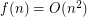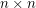More generally, if we let $ f(n) $ denote the size of the smallest $ n $-universal set, we are interested in the behaviour of $ f $. The best known upper bound is $ f(n) = O(n^2) $. Indeed, every $ n $-vertex planar graph can be drawn as required in the $ n \times n $ grid [dFPP], [S]. On the flip side, it is known that 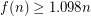$ f(n) \ge 1.098n $ for sufficiently large $ n $ [CH].

Bibliography

[CH] M. Chrobak and H.Karloff. A lower bound on the size of universal sets for planar graphs. SIGACT News, 20:83-86, 1989.

[dFPP] H. de Fraysseix, J. Pach, and R. Pollack. How to draw a planar graph on a grid. Combinatorica, 10(1):41-51, 1990. MathSciNet

[S] W. Schnyder. Embedding planar graphs on the grid. In Proc. 1st ACM-SIAM Sympos. Discrete Algorithms, pages 138-148, 1990.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options