 login/create account
login/create account
Crossing numbers
The Crossing Number of the Complete Graph ★★★
Author(s):
The crossing number 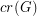 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
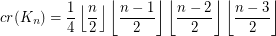
Keywords: complete graph; crossing number
The Crossing Number of the Complete Bipartite Graph ★★★
Author(s): Turan
The crossing number 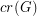 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
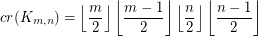
Keywords: complete bipartite graph; crossing number
The Crossing Number of the Hypercube ★★
The crossing number 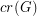 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
The  -dimensional (hyper)cube
-dimensional (hyper)cube 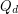 is the graph whose vertices are all binary sequences of length
is the graph whose vertices are all binary sequences of length  , and two of the sequences are adjacent in
, and two of the sequences are adjacent in 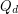 if they differ in precisely one coordinate.
if they differ in precisely one coordinate.
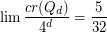
Keywords: crossing number; hypercube
Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
 be the disjoint union of the graphs
be the disjoint union of the graphs 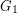 and
and 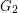 and let
and let 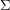 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 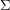 has the property that
has the property that 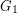 and
and 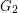 are disjoint?
are disjoint? Keywords: crossing number; surface
Crossing sequences ★★
Author(s): Archdeacon; Bonnington; Siran
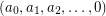 be a sequence of nonnegative integers which strictly decreases until
be a sequence of nonnegative integers which strictly decreases until  .
.
Then there exists a graph that be drawn on a surface with orientable (nonorientable, resp.) genus 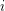 with
with 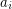 crossings, but not with less crossings.
crossings, but not with less crossings.
Keywords: crossing number; crossing sequence
Crossing numbers and coloring ★★★
Author(s): Albertson
We let 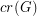 denote the crossing number of a graph
denote the crossing number of a graph  .
.
 with
with 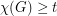 satisfies
satisfies 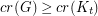 .
. Keywords: coloring; complete graph; crossing number
Are different notions of the crossing number the same? ★★★
 ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
The crossing number 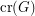 of a graph
of a graph  is the minimum number of edge crossings in any drawing of
is the minimum number of edge crossings in any drawing of  in the plane. In the pairwise crossing number
in the plane. In the pairwise crossing number 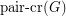 , we minimize the number of pairs of edges that cross.
, we minimize the number of pairs of edges that cross.
Keywords: crossing number; pair-crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University