 login/create account
login/create account
coloring
Crossing numbers and coloring ★★★
Author(s): Albertson
We let 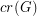 denote the crossing number of a graph
denote the crossing number of a graph  .
.
 with
with 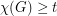 satisfies
satisfies 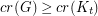 .
. Keywords: coloring; complete graph; crossing number
Are vertex minor closed classes chi-bounded? ★★
Author(s): Geelen
Keywords: chi-bounded; circle graph; coloring; vertex minor
Graphs with a forbidden induced tree are chi-bounded ★★★
Author(s): Gyarfas
Say that a family 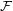 of graphs is
of graphs is 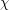 -bounded if there exists a function
-bounded if there exists a function 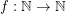 so that every
so that every 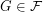 satisfies
satisfies 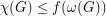 .
.
 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to  is
is 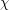 -bounded.
-bounded. Keywords: chi-bounded; coloring; excluded subgraph; tree
Domination in plane triangulations ★★
 has a dominating set of size
has a dominating set of size 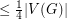 .
. Keywords: coloring; domination; multigrid; planar graph; triangulation
Double-critical graph conjecture ★★
A connected simple graph  is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
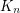 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph Keywords: coloring; complete graph
Counting 3-colorings of the hex lattice ★★
Author(s): Thomassen
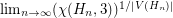 .
. Keywords: coloring; Lieb's Ice Constant; tiling; torus
4-regular 4-chromatic graphs of high girth ★★
Author(s): Grunbaum
Coloring random subgraphs ★★
Author(s): Bukh
If  is a graph and
is a graph and ![$ p \in [0,1] $](/files/tex/1d076f7332523eb59bd7deae19667f83f0a3b6e0.png) , we let
, we let 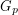 denote a subgraph of
denote a subgraph of  where each edge of
where each edge of  appears in
appears in 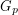 with independently with probability
with independently with probability 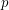 .
.
 so that
so that 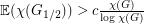 ?
? Keywords: coloring; random graph
Hedetniemi's Conjecture ★★★
Author(s): Hedetniemi
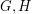 are simple finite graphs, then
are simple finite graphs, then  .
. Here 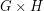 is the tensor product (also called the direct or categorical product) of
is the tensor product (also called the direct or categorical product) of  and
and  .
.
Keywords: categorical product; coloring; homomorphism; tensor product
Degenerate colorings of planar graphs ★★★
Author(s): Borodin
A graph  is
is  -degenerate if every subgraph of
-degenerate if every subgraph of  has a vertex of degree
has a vertex of degree 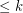 .
.
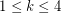 , the union of any
, the union of any  color classes induces a
color classes induces a 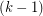 -degenerate graph.
-degenerate graph. Keywords: coloring; degenerate; planar

 Drupal
Drupal CSI of Charles University
CSI of Charles University