 login/create account
login/create account
coloring
Reed's omega, delta, and chi conjecture ★★★
Author(s): Reed
For a graph  , we define
, we define  to be the maximum degree,
to be the maximum degree, 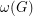 to be the size of the largest clique subgraph, and
to be the size of the largest clique subgraph, and 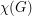 to be the chromatic number of
to be the chromatic number of  .
.
Conjecture 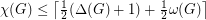 for every graph
for every graph  .
.
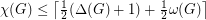 for every graph
for every graph  .
. Keywords: coloring
Grunbaum's Conjecture ★★★
Author(s): Grunbaum
Conjecture If  is a simple loopless triangulation of an orientable surface, then the dual of
is a simple loopless triangulation of an orientable surface, then the dual of  is 3-edge-colorable.
is 3-edge-colorable.
 is a simple loopless triangulation of an orientable surface, then the dual of
is a simple loopless triangulation of an orientable surface, then the dual of  is 3-edge-colorable.
is 3-edge-colorable. Linial-Berge path partition duality ★★★
Conjecture The minimum  -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph.
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Keywords: coloring; directed path; partition

 Drupal
Drupal CSI of Charles University
CSI of Charles University