 login/create account
login/create account
Reed, Bruce A.
Forcing a 2-regular minor ★★
Conjecture Every graph with average degree at least 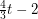 contains every 2-regular graph on
contains every 2-regular graph on 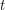 vertices as a minor.
vertices as a minor.
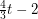 contains every 2-regular graph on
contains every 2-regular graph on 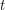 vertices as a minor.
vertices as a minor. Keywords: minors
Fractional Hadwiger ★★
Author(s): Harvey; Reed; Seymour; Wood
Conjecture For every graph  ,
,
(a)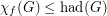
(b)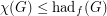
(c)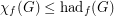 .
.
 ,
,(a)
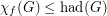
(b)
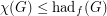
(c)
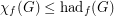 .
. Keywords: fractional coloring, minors
Weighted colouring of hexagonal graphs. ★★
Conjecture There is an absolute constant  such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 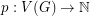 ,
, 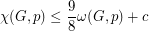
 such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 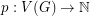 ,
, 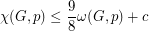
Keywords:
Hoàng-Reed Conjecture ★★★
Conjecture Every digraph in which each vertex has outdegree at least  contains
contains  directed cycles
directed cycles  such that
such that 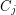 meets
meets 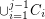 in at most one vertex,
in at most one vertex, 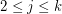 .
.
 contains
contains  directed cycles
directed cycles  such that
such that 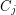 meets
meets 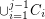 in at most one vertex,
in at most one vertex, 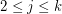 .
. Keywords:
Antidirected trees in digraphs ★★
Author(s): Addario-Berry; Havet; Linhares Sales; Reed; Thomassé
An antidirected tree is an orientation of a tree in which every vertex has either indegree 0 or outdergree 0.
Conjecture Let 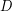 be a digraph. If
be a digraph. If 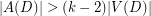 , then
, then 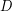 contains every antidirected tree of order
contains every antidirected tree of order  .
.
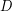 be a digraph. If
be a digraph. If 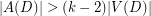 , then
, then 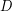 contains every antidirected tree of order
contains every antidirected tree of order  .
. Keywords:
Domination in cubic graphs ★★
Author(s): Reed
Problem Does every 3-connected cubic graph  satisfy
satisfy 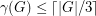 ?
?
 satisfy
satisfy 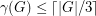 ?
? Keywords: cubic graph; domination
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
Conjecture A triangle-free graph with maximum degree  has chromatic number at most
has chromatic number at most 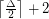 .
.
 has chromatic number at most
has chromatic number at most 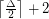 .
.
Keywords: chromatic number; girth; maximum degree; triangle free
Reed's omega, delta, and chi conjecture ★★★
Author(s): Reed
For a graph  , we define
, we define 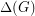 to be the maximum degree,
to be the maximum degree, 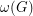 to be the size of the largest clique subgraph, and
to be the size of the largest clique subgraph, and 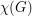 to be the chromatic number of
to be the chromatic number of  .
.
Conjecture 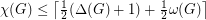 for every graph
for every graph  .
.
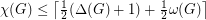 for every graph
for every graph  .
. Keywords: coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University