 login/create account
login/create account
Forcing a 2-regular minor
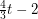 contains every 2-regular graph on
contains every 2-regular graph on 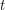 vertices as a minor.
vertices as a minor. Reed and Wood [RW] explained that a result of Corradi and Hajnal [CH] implies that if  is the graph consisting of
is the graph consisting of  disjoint triangles, then every graph with average degree at least
disjoint triangles, then every graph with average degree at least 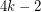 contains
contains  as a minor. Moreover, the bound of
as a minor. Moreover, the bound of 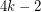 is best possible since the complete bipartite graph
is best possible since the complete bipartite graph 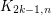 contains no
contains no  -minor, but has average degree tending to
-minor, but has average degree tending to 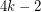 (as
(as 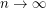 ). Thus the conjecture would generalise this result.
). Thus the conjecture would generalise this result.
Update: There has been a lot of recent progress on this conjecture [HW,CNLWY].
Bibliography
[CH] Keresztely Corradi and Andras Hajnal. On the maximal number of independent circuits of a graph. Acta Math. Acad. Sci. Hungar., 14:423–443, 1963.
*[RW] Bruce Reed and David R. Wood. Forcing a sparse minor, arXiv:1402.0272, 2013.
[HW] Daniel J. Harvey and David R. Wood. Cycles of given size in a dense graph. SIAM J. Discrete Math. 29.4:2336–2349, 2015.
[CNLWY] E. Csóka, S. Norin, I. Lo, H. Wu and L. Yepremyan. The extremal function for disconnected minors. J. Comb. Theory B 126 (2017), 162-174.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University