 login/create account
login/create account
Hoang, Chinh T.
2-colouring a graph without a monochromatic maximum clique ★★
Conjecture If  is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a 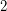 -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic.
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a 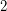 -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
Hoàng-Reed Conjecture ★★★
Conjecture Every digraph in which each vertex has outdegree at least  contains
contains  directed cycles
directed cycles  such that
such that 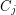 meets
meets 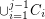 in at most one vertex,
in at most one vertex, 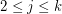 .
.
 contains
contains  directed cycles
directed cycles  such that
such that 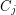 meets
meets 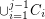 in at most one vertex,
in at most one vertex, 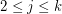 .
. Keywords:
The stubborn list partition problem ★★
Author(s): Cameron; Eschen; Hoang; Sritharan
Problem Does there exist a polynomial time algorithm which takes as input a graph  and for every vertex
and for every vertex 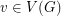 a subset
a subset 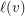 of
of 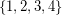 , and decides if there exists a partition of
, and decides if there exists a partition of 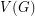 into
into 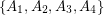 so that
so that 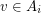 only if
only if 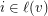 and so that
and so that 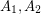 are independent,
are independent, 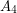 is a clique, and there are no edges between
is a clique, and there are no edges between 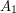 and
and 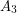 ?
?
 and for every vertex
and for every vertex 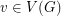 a subset
a subset 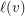 of
of 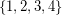 , and decides if there exists a partition of
, and decides if there exists a partition of 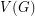 into
into 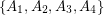 so that
so that 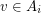 only if
only if 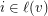 and so that
and so that 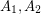 are independent,
are independent, 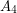 is a clique, and there are no edges between
is a clique, and there are no edges between 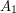 and
and 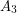 ?
? Keywords: list partition; polynomial algorithm

 Drupal
Drupal CSI of Charles University
CSI of Charles University