 login/create account
login/create account
Hoàng-Reed Conjecture
Conjecture Every digraph in which each vertex has outdegree at least  contains
contains  directed cycles
directed cycles  such that
such that 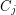 meets
meets 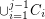 in at most one vertex,
in at most one vertex, 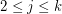 .
.
 contains
contains  directed cycles
directed cycles  such that
such that 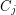 meets
meets 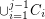 in at most one vertex,
in at most one vertex, 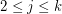 .
. This conjecture is not even known to be true for 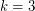 . In the case
. In the case 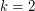 , Thomassen proved [T] that every digraph with minimum outdegree 2 has two directed cycles intersecting on a vertex.
, Thomassen proved [T] that every digraph with minimum outdegree 2 has two directed cycles intersecting on a vertex.
This conjecture would imply the Caccetta-Häggkvist Conjecture.
Bibliography
*[HR] C.T. Hoàng and B. Reed, A note on short cycles in digraphs, Discrete Math., 66 (1987), 103-107.
[T] C. Thomassen, The 2-linkage problem for acyclic digraphs, Discrete Math., 55 (1985), 73-87.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University