 login/create account
login/create account
Tournaments
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
Problem Let  be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path?
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament
Decomposing an even tournament in directed paths. ★★★
Author(s): Alspach; Mason; Pullman
Conjecture Every tournament  on an even number of vertices can be decomposed into
on an even number of vertices can be decomposed into 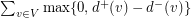 directed paths.
directed paths.
 on an even number of vertices can be decomposed into
on an even number of vertices can be decomposed into 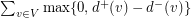 directed paths.
directed paths. Keywords:
Edge-disjoint Hamilton cycles in highly strongly connected tournaments. ★★
Author(s): Thomassen
Conjecture For every 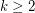 , there is an integer
, there is an integer 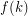 so that every strongly
so that every strongly 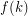 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles.
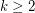 , there is an integer
, there is an integer 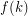 so that every strongly
so that every strongly 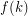 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles. Keywords:
Partitionning a tournament into k-strongly connected subtournaments. ★★
Author(s): Thomassen
Problem Let  be positve integer Does there exists an integer
be positve integer Does there exists an integer  such that every
such that every  -strong tournament
-strong tournament  admits a partition
admits a partition 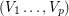 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 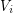 is a non-trivial
is a non-trivial  -strong for all
-strong for all 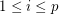 .
.
 be positve integer Does there exists an integer
be positve integer Does there exists an integer  such that every
such that every  -strong tournament
-strong tournament  admits a partition
admits a partition 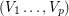 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 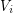 is a non-trivial
is a non-trivial  -strong for all
-strong for all 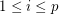 .
. Keywords:
Decomposing k-arc-strong tournament into k spanning strong digraphs ★★
Author(s): Bang-Jensen; Yeo
Conjecture Every k-arc-strong tournament decomposes into k spanning strong digraphs.
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University