 login/create account
login/create account
triangle free
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
Conjecture A triangle-free graph with maximum degree 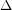 has chromatic number at most
has chromatic number at most 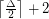 .
.
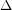 has chromatic number at most
has chromatic number at most 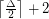 .
.
Keywords: chromatic number; girth; maximum degree; triangle free
Non-edges vs. feedback edge sets in digraphs ★★★
Author(s): Chudnovsky; Seymour; Sullivan
For any simple digraph  , we let
, we let 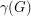 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 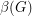 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
Conjecture If  is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 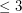 , then
, then 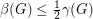 .
.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 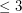 , then
, then 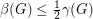 .
. Keywords: acyclic; digraph; feedback edge set; triangle free
Circular coloring triangle-free subcubic planar graphs ★★
Problem Does every triangle-free planar graph of maximum degree three have circular chromatic number at most 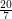 ?
?
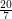 ?
? Keywords: circular coloring; planar graph; triangle free
Unions of triangle free graphs ★★★
Problem Does there exist a graph with no subgraph isomorphic to 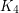 which cannot be expressed as a union of
which cannot be expressed as a union of 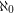 triangle free graphs?
triangle free graphs?
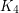 which cannot be expressed as a union of
which cannot be expressed as a union of 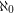 triangle free graphs?
triangle free graphs? Keywords: forbidden subgraph; infinite graph; triangle free
Triangle free strongly regular graphs ★★★
Author(s):
Problem Is there an eighth triangle free strongly regular graph?
Keywords: strongly regular; triangle free

 Drupal
Drupal CSI of Charles University
CSI of Charles University