 login/create account
login/create account
Triangle free strongly regular graphs
A regular graph  is strongly regular if there exist integers
is strongly regular if there exist integers 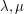 so that every pair of adjacent vertices have exactly
so that every pair of adjacent vertices have exactly  common neighbors, and every pair of nonadjacent vertices have exactly
common neighbors, and every pair of nonadjacent vertices have exactly  common neighbors. To eliminate degeneracies, we shall further assume that
common neighbors. To eliminate degeneracies, we shall further assume that 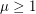 . If
. If  is
is  -regular and
-regular and  , then we say that
, then we say that  is a
is a 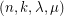 strongly regular graph.
strongly regular graph.
There are exactly seven triangle-free strongly regular graphs known: The five cycle, the Petersen Graph, The Clebsch Graph, the Hoffman-Singleton Graph, The Gewirtz Graph, the Higman-Sims Graph, and a  strongly regular subgraph of the Higman-Sims graph. Every Moore Graph of diameter 2 is a triangle-free strongly regular graph, so if there is a 57-regular Moore Graph of diameter 2, this would add another to the list.
strongly regular subgraph of the Higman-Sims graph. Every Moore Graph of diameter 2 is a triangle-free strongly regular graph, so if there is a 57-regular Moore Graph of diameter 2, this would add another to the list.
See Andries Brouwer's graph descriptions for more on these graphs.
Bibliography
[G] C. D. Godsil, Problems in Algebraic Combinatorics, Electronic Journal of Combinatorics, Volume 2, F1
* indicates original appearance(s) of problem.
Reply..
I hate math..Lol _________________________________________________________________________________________ toll free number
The complement of $2 K_n$
The complement of 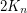 is triangle free srg with parameters
is triangle free srg with parameters 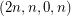 . Probably this infinite case should be excluded from the conjecture.
. Probably this infinite case should be excluded from the conjecture.
If the number of the
If the number of the vertices are even, we can determine regular triangle free graphs up to half the number of vertices of any degree. However, this does not hold true if the vertices numbers are odd. Some of the examples of even vertices graphs are Petersen graph (10 vertices), Heawood graph (14 vertices), Clebsch graph (16 vertices), Pappus graph (18 vertices) and odd vertices graph includes Schläfli graph (27 vertices), Perkel graph (57 vertices). 800 numbers

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Higman-Sims Graph
In fact, all (seven) known primitive triangle-free strongly regular graphs are actual *subgraphs* of the Higman-Sims graph (which btw was first constructed by Dale Mesner). A Moore graph of degree 57 would of course break this mold.