 login/create account
login/create account
For any simple digraph  , we let
, we let 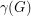 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 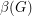 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 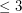 , then
, then 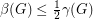 .
. If  satisfies
satisfies  , then
, then  is a tournament, and it is easy to check that
is a tournament, and it is easy to check that  will have a directed cycle of length three unless it is acyclic, in which case
will have a directed cycle of length three unless it is acyclic, in which case 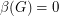 . So in this case, the conjecture holds. More generally, it is natural to suspect that a digraph with few non-edges and no directed triangles should be close to acyclic. Indeed, this conjecture asserts a precise relationship of this form.
. So in this case, the conjecture holds. More generally, it is natural to suspect that a digraph with few non-edges and no directed triangles should be close to acyclic. Indeed, this conjecture asserts a precise relationship of this form.
If true, the above conjecture is essentially tight for a number of examples. We noted above that it is tight for transitive tournaments. Here is another basic class: let  be the circulant digraph obtained by placing
be the circulant digraph obtained by placing 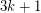 vertices in a circle, and adding an edge directed from
vertices in a circle, and adding an edge directed from  to
to  whenever
whenever  is distance
is distance 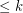 from
from  in the clockwise order. Such examples may be nested to obtain new ones.
in the clockwise order. Such examples may be nested to obtain new ones.
Chudnovsky, Seymour, and Sullivan [CSS] utilized a clever double counting argument to prove that  always holds. They also proved their conjecture in the case when
always holds. They also proved their conjecture in the case when 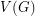 is the union of two cliques, and when
is the union of two cliques, and when  is a circular interval digraph.
is a circular interval digraph.
Bibliography
*[CSS] M. Chudnovsky, P.D. Seymour, and B. Sullivan, Cycles in dense digraphs.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University