 login/create account
login/create account
chromatic number
Cycles in Graphs of Large Chromatic Number ★★
Author(s): Brewster; McGuinness; Moore; Noel
Conjecture If 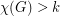 , then
, then  contains at least
contains at least 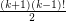 cycles of length
cycles of length 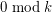 .
.
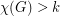 , then
, then  contains at least
contains at least 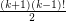 cycles of length
cycles of length 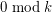 .
. Keywords: chromatic number; cycles
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
Conjecture If  is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
.
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
Choosability of Graph Powers ★★
Author(s): Noel
Question (Noel, 2013) Does there exist a function 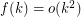 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
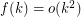 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
Keywords: choosability; chromatic number; list coloring; square of a graph
Ohba's Conjecture ★★
Author(s): Ohba
Conjecture If 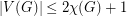 , then
, then 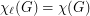 .
.
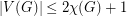 , then
, then 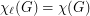 .
. Keywords: choosability; chromatic number; complete multipartite graph; list coloring
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
Conjecture A triangle-free graph with maximum degree  has chromatic number at most
has chromatic number at most 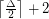 .
.
 has chromatic number at most
has chromatic number at most 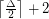 .
.
Keywords: chromatic number; girth; maximum degree; triangle free

 Drupal
Drupal CSI of Charles University
CSI of Charles University