 login/create account
login/create account
Noel, Jonathan A.
Weak saturation of the cube in the clique ★
Determine 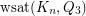 .
.
Keywords: bootstrap percolation; hypercube; Weak saturation
Extremal $4$-Neighbour Bootstrap Percolation in the Hypercube ★★
 -neighbour bootstrap process in the hypercube.
-neighbour bootstrap process in the hypercube. Keywords: bootstrap percolation; extremal combinatorics; hypercube; percolation
Saturation in the Hypercube ★★
Author(s): Morrison; Noel; Scott
 in the
in the  -dimensional hypercube?
-dimensional hypercube? Keywords: cycles; hypercube; minimum saturation; saturation
Cycles in Graphs of Large Chromatic Number ★★
Author(s): Brewster; McGuinness; Moore; Noel
 , then
, then  contains at least
contains at least 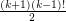 cycles of length
cycles of length 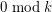 .
. Keywords: chromatic number; cycles
Saturated $k$-Sperner Systems of Minimum Size ★★
Author(s): Morrison; Noel; Scott
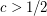 and a function
and a function 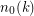 such that if
such that if 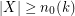 , then every saturated
, then every saturated  -Sperner system
-Sperner system 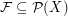 has cardinality at least
has cardinality at least 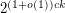 ?
? Keywords: antichain; extremal combinatorics; minimum saturation; saturation; Sperner system
Partitioning the Projective Plane ★★
Author(s): Noel
Throughout this post, by projective plane we mean the set of all lines through the origin in 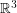 .
.
 of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin.  of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 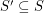 such that
such that  is octahedral.
is octahedral. 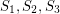 and
and  such that each set
such that each set  is weakly octahedral. Then each
is weakly octahedral. Then each  is octahedral.
is octahedral. Keywords: Partitioning; projective plane
Choosability of Graph Powers ★★
Author(s): Noel
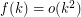 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
Keywords: choosability; chromatic number; list coloring; square of a graph
Choice Number of k-Chromatic Graphs of Bounded Order ★★
Author(s): Noel
 is a
is a  -chromatic graph on at most
-chromatic graph on at most 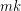 vertices, then
vertices, then 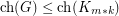 .
. Keywords: choosability; complete multipartite graph; list coloring
Mixing Circular Colourings ★
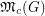 always rational?
always rational? Keywords: discrete homotopy; graph colourings; mixing

 Drupal
Drupal CSI of Charles University
CSI of Charles University