Home » Subject » Geometry
Importance: Medium ✭✭
Author(s): Noel, Jonathan A.
Subject: Geometry
Keywords: Partitioning
projective plane
Recomm. for undergrads: yes
Posted by: Jon Noel
on: August 27th, 2013

Throughout this post, by projective plane we mean the set of all lines through the origin in 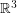$ \mathbb{R}^3 $.

Definition   Say that a subset $ S $ of the projective plane is octahedral if all lines in $ S $ pass through the closure of two opposite faces of a regular octahedron centered at the origin.
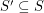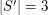Definition   Say that a subset $ S $ of the projective plane is weakly octahedral if every set $ S'\subseteq S $ such that $ |S'|=3 $ is octahedral.
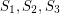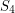Conjecture   Suppose that the projective plane can be partitioned into four sets, say $ S_1,S_2,S_3 $ and $ S_4 $ such that each set 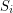$ S_i $ is weakly octahedral. Then each 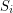$ S_i $ is octahedral.

Also, see the posting on mathoverflow.

There is an equivalent definition of the "weakly octahedral" condition which may be useful.

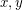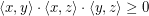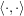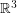Lemma   A subset $ S $ of the projective plane is weakly octahedral if for any three lines in $ S $ and any three vectors $ x, y $ and $ z $ which span these lines, we have $$\langle x,y\rangle \cdot\langle x,z\rangle \cdot\langle y,z\rangle \geq 0$$ where $ \langle\cdot,\cdot\rangle $ is the standard (dot) inner product on $ \mathbb{R}^3 $.

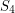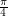The fact that $ S_1,S_2,S_3 $ and $ S_4 $ partition the projective plane seems to be important. Here is an example of a weakly octahedral set that is not octahedral: Fix any vector $ x $ and let $ S $ be the set of all lines which are spanned by vectors which meet $ x $ at an angle strictly less than $ \frac{\pi}{4} $.

This question came up while working on another problem posted to this site: Circular colouring the orthogonality graph. It is possible that a solution to the problem stated here can be applied to solve this problem. Moreover, it may be useful in proving that the real orthogonality graph (defined in the other posting) has (essentially) only one proper $ 4 $-colouring.

Related problems

Circular colouring the orthogonality graph
The Double Cap Conjecture

Bibliography



* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options