 login/create account
login/create account
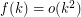 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
For a survey of choosability, including relevant definitions, see [Noe] or click here.
The List Square Colouring Conjecture, due to Kostochka and Woodall [KW], states that  for every graph
for every graph  . This was disproved by Kim and Park [KP], who proved that there is a sequence
. This was disproved by Kim and Park [KP], who proved that there is a sequence 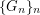 of graphs and a constant
of graphs and a constant 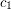 such that
such that 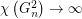 and
and  for all
for all  . To obtain this lower bound from the construction of Kim and Park, one can apply the well-known result of Alon [Alo].
. To obtain this lower bound from the construction of Kim and Park, one can apply the well-known result of Alon [Alo].
It may be the case that the correct upper bound for all graphs is of the same order of magnitude as the example in the result of Kim and Park.
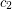 such that every graph
such that every graph  satisfies
satisfies 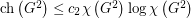 ?
? By calculating the clique number and maximum degree of 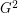 , one can easily show that
, one can easily show that  (this observation is due to Young Soo Kwon), but it seems that no significantly better bound is known.
(this observation is due to Young Soo Kwon), but it seems that no significantly better bound is known.
 contains an edge, then
contains an edge, then ![\[\text{ch}\left(G^2\right)< \chi\left(G^2\right)^2.\]](/files/tex/55607e4235adb09b912325f05596eb57c93a6488.png)
![\[\chi\left(G^2\right) \geq \omega\left(G^2\right) \geq \Delta(G)+1,\]](/files/tex/965a2b7eaa9b0d6d50962e4ab8a5ef1d4f743ade.png)
![\[\text{ch}\left(G^2\right) \leq \Delta\left(G^2\right)+1 \leq \Delta(G)\left(\Delta(G)-1\right) + \Delta(G)+1 = \Delta(G)^2+1.\]](/files/tex/af60d139a2cbb9e77e9e64b676531c124b8dbe07.png) Therefore, since
Therefore, since 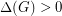 , we have
, we have ![\[\text{ch}\left(G^2\right)\leq \Delta(G)^2+1 < \left(\Delta(G)+1\right)^2 \leq \chi\left(G^2\right)^2.\]](/files/tex/be710781dba7f6c91db094cd9f385e7e7555d307.png) This completes the proof.
This completes the proof. These questions are related to a problem of Zhu (see Doug West's webpage for more info) who asked whether there exists an integer  such that for every graph
such that for every graph  , we have that
, we have that 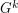 has choice number equal to chromatic number. This conjecture has been disproved independently by Kim, Kwon and Park [KKP] and Kosar, Petrickova, Reigniger and Yeager [KPRY]. The example of [KPRY] also yields, for every
has choice number equal to chromatic number. This conjecture has been disproved independently by Kim, Kwon and Park [KKP] and Kosar, Petrickova, Reigniger and Yeager [KPRY]. The example of [KPRY] also yields, for every  , a sequence
, a sequence 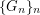 of graphs and a constant
of graphs and a constant  such that
such that 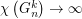 and
and 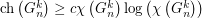 for all
for all  . They ask the following, more general, questions:
. They ask the following, more general, questions:
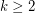 , does there exist a function
, does there exist a function  such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^k\right)\leq f_k\left(\chi\left(G^k\right)\right)?\]](/files/tex/7effce50c8fecbbaace45cbcdbcd4bdefd187fdd.png)
To our knowledge, it is not known whether there exists a function 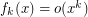 such that the same conclusion holds. (Intuitively, it seems that higher values of
such that the same conclusion holds. (Intuitively, it seems that higher values of  should yield a smaller separation between
should yield a smaller separation between 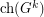 and
and 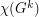 ; however, there seems to be no hard evidence to support this.)
; however, there seems to be no hard evidence to support this.)
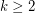 , does there exist a positive constant
, does there exist a positive constant  such that every graph
such that every graph  satisfies
satisfies 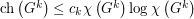 ? Moreover, can the constant
? Moreover, can the constant  be made independent of
be made independent of  ?
? These questions are also related to the so-called List Total Colouring Conjecture of Borodin, Kostochka and Woodall [BKW], which says that the total graph of a multigraph always satisfies  . Given a multigraph
. Given a multigraph  , the total graph of
, the total graph of  can be obtained by subdividing every edge of
can be obtained by subdividing every edge of  and then taking the square of the resulting graph.
and then taking the square of the resulting graph.
Bibliography
[Alo] Noga Alon. Choice numbers of graphs: a probabilistic approach. Combin. Probab. Comput., 1(2):107–114, 1992.
[BKW] Oleg V. Borodin, Alexandr V. Kostochka, and Douglas R. Woodall. List edge and list total colourings of multigraphs. J. Combin. Theory Ser. B, 71(2):184–204, 1997.
[KP] Seog-Jin Kim and Boram Park: Counterexamples to the List Square Coloring Conjecture, submitted.
[KKP] Seog-Jin Kim, Young Soo Kwon and Boram Park: Chromatic-choosability of the power of graphs.
[KPRY] Nicholas Kosar, Sarka Petrickova, Benjamin Reiniger, Elyse Yeager: A note on list-coloring powers of graphs.
[KW] Alexandr V. Kostochka and Douglas R. Woodall. Choosability conjectures and multicircuits, Discrete Math., 240 (2001), 123--143.
[Noe] Jonathan A. Noel. Choosability of Graphs with Bounded Order: Ohba's Conjecture and Beyond, Master's thesis. McGill University (2013). pdf.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University