Home » Subject » Combinatorics
Importance: Medium ✭✭
Author(s): Morrison, Natasha
Noel, Jonathan A.
Subject: Combinatorics
Keywords: bootstrap percolation
extremal combinatorics
hypercube
percolation
Recomm. for undergrads: no
Posted by: Jon Noel
on: September 20th, 2015
Problem   Determine the smallest percolating set for the $ 4 $-neighbour bootstrap process in the hypercube.

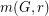The $ r $-neighbour bootstrap process starts with an initial set of "infected" vertices in a graph and, at each step, a healthy vertex becomes infected if it has at least $ r $ infected neighbours. Say that the initial set of infected vertices percolates if every vertex of $ G $ is eventually infected. Let $ m(G,r) $ denote the smallest percolating set in $ G $ under the $ r $-neighbour process.

Let 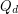$ Q_d $ denote the hypercube of dimension $ d $. Balogh and Bollobás [BB] proved the following.

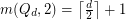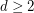Theorem  (Balogh and Bollobás)   $ m(Q_d,2) = \left\lceil \frac{d}{2}\right\rceil +1 $ for all $ d\geq 2 $.

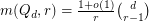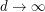They also conjectured that $ m(Q_d,r) = \frac{1+o(1)}{r}\binom{d}{r-1} $ for fixed $ r $ and $ d\to\infty $. This conjecture was proved by Morrison and Noel [MN], who also showed the following.

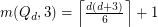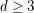Theorem  (Morrison and Noel)   $ m(Q_d,3) = \left\lceil \frac{d(d+3)}{6} \right\rceil +1 $ for all $ d\geq 3 $.

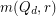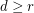It seems possible that one could obtain a general formula for $ m(Q_d,r) $ for all $ r $ and $ d\geq r $. However, the precise formula for 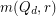$ m(Q_d,r) $ (in terms of $ d $) is not known for any fixed 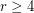$ r\geq4 $. A solution to this problem may have applications in proving probabilistic results for bootstrap percolation in the hypercube; see [BBM].

Bibliography

[BB] J. Balogh and B. Bollobás, Bootstrap percolation on the hypercube, Probab. Theory Related Fields 134 (2006), no. 4, 624–648.

[BBM] J. Balogh, B. Bollobás and R. Morris, Bootstrap percolation in high dimensions, Combin. Probab. Comput. 19 (2010), no. 5-6, 643–692.

[MN] N. Morrison and J. A. Noel, Extremal Bounds for Bootstrap Percolation in the Hypercube, preprint, arXiv:1506.04686v1.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options