 login/create account
login/create account
Linial, Nathan
Signing a graph to have small magnitude eigenvalues ★★
Conjecture If  is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 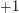 entries by
entries by  ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 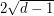 .
.
 is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 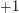 entries by
entries by  ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 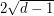 .
. Keywords: eigenvalue; expander; Ramanujan graph; signed graph; signing
Linial-Berge path partition duality ★★★
Conjecture The minimum  -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph.
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Keywords: coloring; directed path; partition
The Alon-Tarsi basis conjecture ★★
Author(s): Alon; Linial; Meshulam
Conjecture If  are invertible
are invertible 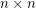 matrices with entries in
matrices with entries in  for a prime
for a prime 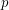 , then there is a
, then there is a 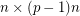 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base.
 are invertible
are invertible 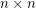 matrices with entries in
matrices with entries in  for a prime
for a prime 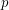 , then there is a
, then there is a 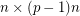 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base. Keywords: additive basis; matrix
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
Conjecture For every prime 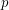 , there is a constant
, there is a constant 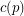 (possibly
(possibly 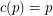 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 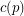 bases of the vector space
bases of the vector space 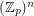 contains an additive basis.
contains an additive basis.
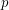 , there is a constant
, there is a constant 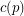 (possibly
(possibly 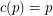 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 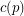 bases of the vector space
bases of the vector space 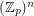 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix

 Drupal
Drupal CSI of Charles University
CSI of Charles University