 login/create account
login/create account
Alon, Noga
Arc-disjoint directed cycles in regular directed graphs ★★
Author(s): Alon; McDiarmid; Molloy
 is a
is a  -regular directed graph with no parallel arcs, then
-regular directed graph with no parallel arcs, then  contains a collection of
contains a collection of 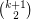 arc-disjoint directed cycles.
arc-disjoint directed cycles. Keywords:
PTAS for feedback arc set in tournaments ★★
Keywords: feedback arc set; PTAS; tournament
List chromatic number and maximum degree of bipartite graphs ★★
Author(s): Alon
 such that the list chromatic number of any bipartite graph
such that the list chromatic number of any bipartite graph  of maximum degree
of maximum degree  is at most
is at most 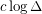 .
.
Keywords:
Splitting a digraph with minimum outdegree constraints ★★★
Author(s): Alon
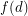 such that the vertices of any digraph with minimum outdegree
such that the vertices of any digraph with minimum outdegree  can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least
can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least  ?
? Keywords:
Nearly spanning regular subgraphs ★★★
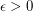 and every positive integer
and every positive integer  , there exists
, there exists 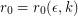 so that every simple
so that every simple  -regular graph
-regular graph  with
with 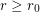 has a
has a  -regular subgraph
-regular subgraph  with
with 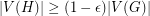 .
. Even vs. odd latin squares ★★★
A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.
 , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different. Keywords: latin square
Ramsey properties of Cayley graphs ★★★
Author(s): Alon
 so that every abelian group
so that every abelian group  has a subset
has a subset 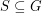 with
with 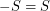 so that the Cayley graph
so that the Cayley graph 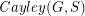 has no clique or independent set of size
has no clique or independent set of size 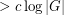 .
. Keywords: Cayley graph; Ramsey number
Alon-Saks-Seymour Conjecture ★★★
Author(s): Alon; Saks; Seymour
 is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 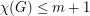 .
. Keywords: coloring; complete bipartite graph; eigenvalues; interlacing
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
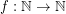 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets  so that for
so that for 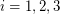 , every component of the graph induced by
, every component of the graph induced by 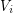 has size at most
has size at most 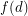 ?
? Keywords: coloring; partition; planar graph
Strong colorability ★★★
Author(s): Aharoni; Alon; Haxell
Let  be a positive integer. We say that a graph
be a positive integer. We say that a graph  is strongly
is strongly  -colorable if for every partition of the vertices to sets of size at most
-colorable if for every partition of the vertices to sets of size at most  there is a proper
there is a proper  -coloring of
-coloring of  in which the vertices in each set of the partition have distinct colors.
in which the vertices in each set of the partition have distinct colors.
 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 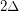 -colorable.
-colorable. Keywords: strong coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University