Home » Subject » Graph Theory » Graph Algorithms

PTAS for feedback arc set in tournaments

Importance: Medium ✭✭
Author(s): Ailon, Nir
Alon, Noga
Subject: Graph Theory
» Graph Algorithms
Keywords: feedback arc set
PTAS
tournament
Recomm. for undergrads: no
Posted by: fhavet
on: March 15th, 2013
Question   Is there a polynomial time approximation scheme for the feedback arc set problem for the class of tournaments?

A tournament is an orientation of a complete graph. A feedback arc set is a set of arcs in a digraph whose removal leave the digraph acyclic. The feedback arc set problem consists in finding a feedback arc set of minimum size. A polynomial time approximation scheme is an algorithm which takes an instance of an optimization problem and a parameter 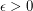$ \epsilon > 0 $ and, in polynomial time, produces a solution that is within a factor 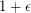$ 1+\epsilon $ of being optimal.

The feedback arc set problem has been proved NP-hard. See [ACM, A, CTY, C]. It was shown in [RS] that the feedback arc set problem is fixed parameter tractable for tournaments.

Bibliography

*[AA] N. Ailon, N. Alon, link, Inform. and Comput. 205 (8) (2007) 1117–1129.

[ACM] N. Alion, M. Charikar, A. Newman, Aggregating inconsistent information: Ranking and clustering, in: Proceedings of the 37th Symposium on the Theory of Computing, STOC, ACM Press, 2005, pp. 684–693.

[A] N. Alon, Ranking tournaments, SIAM J. Discrete Math. 20 (2006) 137–142.

[CTY] P. Charbit, P. Thomassé, A. Yeo, The minimum Feedback arc set problem is NP-hard for tournaments, Combin. Probab. Comput. 16 (1) (2007) 1–4.

[C] V. Conitzer, Computing Slater rankings using similarities among candidates, in: Proceedings, The Twenty-First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference, July 16–20, AAAI Press, Boston, Massachusetts, USA, 2006.

[RS] V. Raman, S. Saurabh, Parameterized complexity of directed feedback arc set problems in tournaments, in: Algorithms and Data Structures, in: Lecture Notes in Computer Science, vol. 2748, Springer, Berlin, 2003, pp. 484–492.


* indicates original appearance(s) of problem.
add new comment